javascript浮點數的陷阱
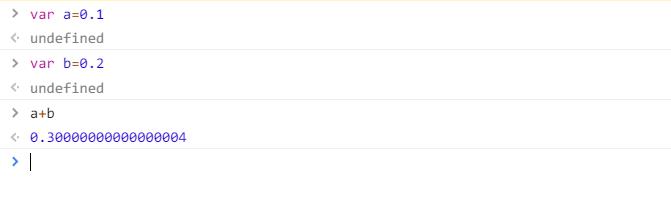
0.1+0.2是多少?相信每個人一定可以毫不猶豫且馬上說出是0.3,沒錯答案就是0.3
記得高中的數學期中考一定會考這樣的證明題
已知1/3=0.33333333…………
1/3*3=1
0.33333333………… *3= 0.99999999…………
最後1/3乘以3和0.3333乘以3會有微小的0.000000001的誤差。
實際上答案就是 0.99999999…………的無限循環,只是我們習慣忽略微小的誤差,直接將答案進位為1。
但是電腦無法忽略微小的誤差,對於電腦來說, 0.33333333………… *3就是 0.99999999…………,永遠不會是1,答案如果出現1,就是為了符合人類的習慣去調整誤差,讓他變成簡單的1
在javascript中,浮點數的運算都會遇到這個誤差的問題,例如一開始所問的0.1+0.2,實際上javascript運算的時候可能為0.10000000000000001+0.20000000000000003,所以相加答案為0.30000000000000004,可是這並不是我們想要的答案,我們想要的答案只是單純的0.3,要如何讓javascript的浮點數運算可以符合人類的直覺運算呢?
如何解決javascript浮點數的問題?
使用toFixed()方法:
指定小數點之後幾位數,例如:
1.9487.toFixed(2) //1.95取小數點後兩位,第二位以後四捨五入。
這是一個快速方便的方法,卻不是最完美的解決方法,這個方法還是有浮點數的陷阱的,例如:
1.005.toFixed(2) //1.001.005取小數點後兩位,第三位四捨五入結果應該是1.01才對,結果出來竟然是1.00,原因一樣是javascript的浮點數陷阱。實際上,1.005是1.00499999999999989,所以四捨五入之後會變成1.00
如果不是很在意小數點相差的一點點數字,這是個快速又方便的好方法。但是如果真的很重視數字的精確度,一分一毫都不可以誤差,該要如何呢?這時候可以試試這個方法
使用toPrecision()方法:
指定要顯示幾位數字(範圍為:1~21),並且將結果以字串回傳
如果數字是小數點,就會用0去補足
0.1.toPrecision(5) // "0.10000"如果數字是小數但位數不足,一樣會四捨五入
12.3456.toPrecision(5) //"12.346"如果數字是整數但位數不足,則會轉換為指數的寫法
10000.toPrecision(4) //"1.000e+4"(這部份看不太懂,所以無法詳細描述,但是還是有一個範例)
所以如果要解決浮點數相加相減的問題,可以這麼做
(0.1+0.2).toPrecision(12) //'0.3'至於為什麼參數要帶12,因為12位可以避免大部分浮點數的問題
基本上使用toProcision()就可以解決浮點數相加相減的陷阱,但是要特別注意到,toPercision回傳的結果是字串,不是數字。
雖然javascript是弱型別的語言,可以任意自動轉換型別,但是難保哪天型別轉換會發生錯誤,反而要花更多時間去除錯,所以事先轉換好型別,讓未來少點除錯的功夫
因此使用parseFloat()方法
parseFloat((0.1+0.2).toPrecision(12)) //0.3parseFloat會將字串轉換成數字,如果不能轉換成數字,則回傳NaN
這樣一來,javascript浮點數的陷阱就算是漂亮的避開囉
